Diffusion & Flow Matching Part 1: Introduction
- Diffusion models gradually add noise to data, then learn to reverse the process
- Flow matching learns a velocity field that directly transports noise to data
- Both achieve state-of-the-art results; flow matching is often simpler to train
Series Overview
This multi-part series explores the theory behind modern generative models. Each post builds on the previous one:
| Part | Topic | What You’ll Learn |
|---|---|---|
| Part 1 | Introduction (this post) | High-level overview of diffusion and flow matching |
| Part 2 | Understanding Flows | Vector fields, trajectories, and flows — the foundation |
| Part 3 | Probability Paths | How we define paths from noise to data |
| Part 4 | The Flow Matching Loss | The marginalization trick that makes training work |
| Part 5 | Diffusion Models & SDEs | Stochastic differential equations and Brownian motion |
| Part 6 | Score Functions | Conditional and marginal scores, the training trick |
| Part 7 | Training Algorithms | CFM, DDPM, and the conversion formulas |
| Part 8 | Guided Generation | Classifier and classifier-free guidance |
| Part 9 | U-Net Architecture | The workhorse architecture for image generation |
| Part 10 | Diffusion Transformers | DiT: Transformers for diffusion |
| Part 11 | Building an Image Generator | Hands-on: train a flow matching model on CIFAR-10 |
| Part 12 | Why Diffusion? | The multimodal problem — why direct regression fails |
What Are We Building?
Diffusion models and flow matching power today’s best generative AI systems — Stable Diffusion, DALL-E, Midjourney, and Flux. Despite their different formulations, both solve the same fundamental problem:
How do we learn to transform random noise into structured data?
You might wonder: why all this complexity? Can’t we just train a network to map labels to images directly? The short answer is mode averaging — direct regression produces blurry outputs when multiple valid answers exist. See Part 12: Why Diffusion? for the full explanation.
If we can do this, we can generate new images, audio, video, or any data type by starting with random noise and “flowing” toward realistic samples.
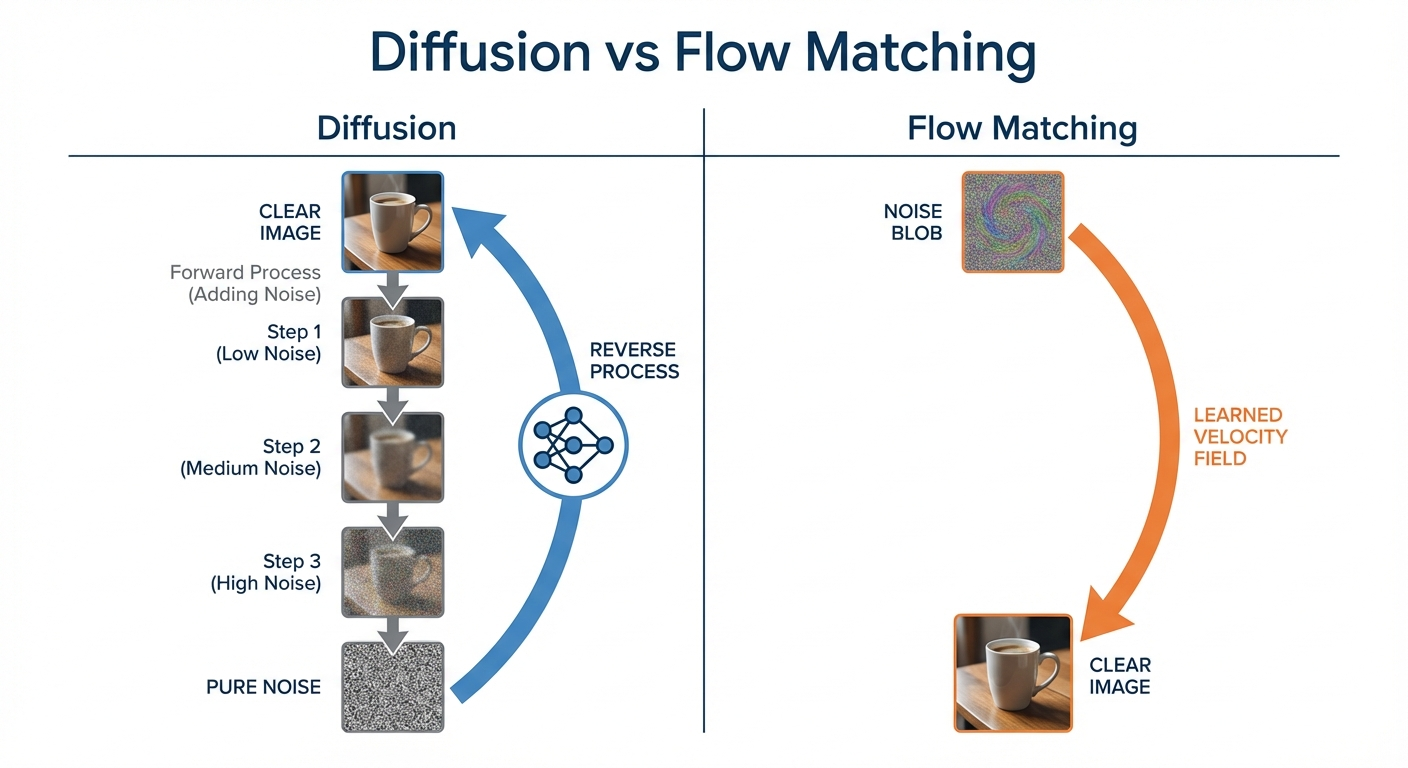
Diffusion Models: The Noisy Path
The key idea behind diffusion models is surprisingly simple:
- Forward process: Take real data and gradually corrupt it with noise until it becomes pure random noise
- Reverse process: Train a neural network to undo this corruption step by step
Think of it like this: if you slowly blur a photograph until it’s unrecognizable static, the neural network learns to “unblur” it. At generation time, you start with pure static and apply the learned unblurring process to create a new image.
The forward process is fixed (just adding noise), so the only thing we need to learn is how to reverse it. The network is trained to predict how much noise was added at each step.
Flow Matching: The Direct Path
Flow matching takes a more direct approach:
- Define a path: Specify how to smoothly interpolate between noise and data
- Learn the velocity: Train a neural network to predict the direction of motion along this path
Imagine dropping a leaf into a river. The current (vector field) tells the leaf which way to move at each moment. If we design the currents correctly, leaves dropped anywhere in the “noise region” will flow toward the “data region.”
The simplest path is a straight line between a noise sample and a data sample. The network learns the velocity field that produces these straight-line trajectories.
How Do They Compare?
| Aspect | Diffusion | Flow Matching |
|---|---|---|
| Corruption process | Gradual noise addition | Direct interpolation |
| What the network learns | How much noise to remove | Which direction to move |
| Sampling method | Iterative denoising | Following the learned flow |
| Underlying theory | Score matching | Optimal transport |
| Path type | Stochastic (random) | Deterministic (fixed) |
The Deep Connection
Despite their different presentations, diffusion and flow matching are deeply related. Every diffusion model has an equivalent “probability flow” formulation that looks like flow matching. The score function (gradient of log probability) in diffusion corresponds to the velocity field in flow matching.
This connection means insights from one framework often transfer to the other, and modern systems sometimes combine ideas from both.
We’ve seen two paradigms for generative modeling: diffusion (add noise, learn to denoise) and flow matching (learn a velocity field that transports noise to data). Despite their different motivations, they share deep mathematical structure — every diffusion model has an equivalent ODE formulation.
This series will make these connections precise. We’ll build up the theory piece by piece: first understanding what flows are (Part 2), then constructing probability paths (Part 3), deriving training losses (Part 4), adding stochasticity (Part 5), and finally connecting everything through score functions (Parts 6-7).
What’s Next?
In the following posts, we’ll develop the mathematical machinery to understand these methods properly:
- Part 2: We’ll define what “flows” and “vector fields” actually mean
- Part 3: We’ll see how to construct paths from noise to data
- Part 4: We’ll discover the clever trick that makes training tractable
- Part 5: We’ll add stochasticity to get SDEs and understand Brownian motion
- Part 6: We’ll learn about score functions and the training trick
By the end, you’ll understand not just what these models do, but why they work.