Flows Explained Simply: A Visual Guide

Flow

Intuition: Think of a River

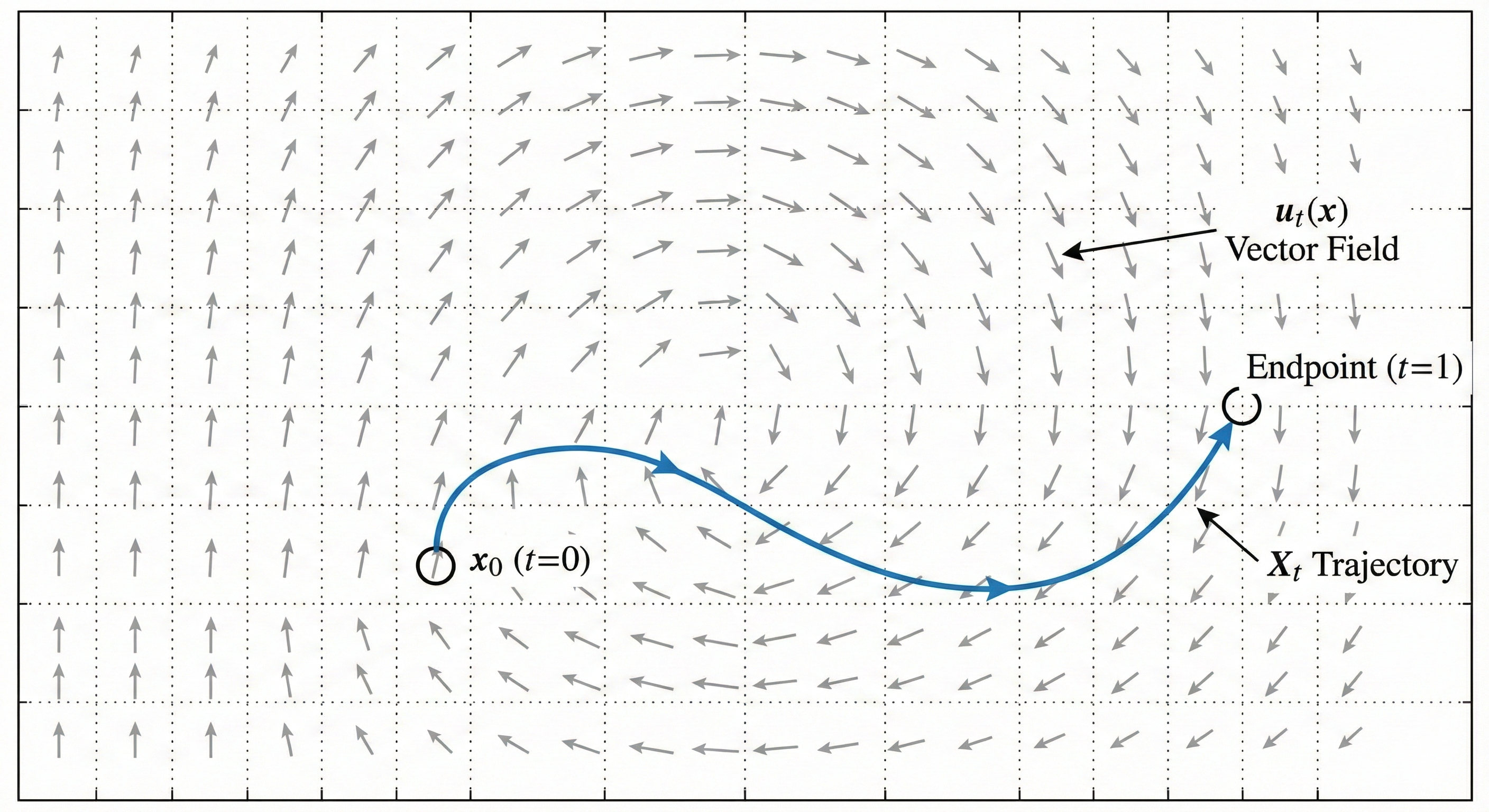
Imagine a river with currents flowing in different directions at different locations.

• Vector field \(u_t(x)\): The current at each point — it tells a particle “if you’re here, move in this direction”
• Trajectory \(X_t\): Following one leaf dropped in the river — where is that specific leaf at time \(t\)?
• Flow \(\phi_t(x)\): A map that answers “where does any leaf end up at time \(t\), given it started at position \(x\)?”

The key insight: \(X_t\) tracks one particle, while \(\phi_t\) describes how the entire space transforms over time.

Figure 1: A single trajectory following the vector field

Formal Definition

Every ODE is defined by a vector field \(u_t(x)\). A solution \(X_t\) starting from \(x_0\) must satisfy:

\[ \begin{aligned} \frac{dX_t}{dt} &= u_t(X_t) \\ X_0 &= x_0 \quad (\text{initial condition}) \end{aligned} \tag{1}\]

In words: “your velocity equals whatever the vector field says at your current location.”

From Trajectory to Flow

The trajectory \(X_t\) answers: “where am I at time \(t\), given I started at \(x_0\)?”

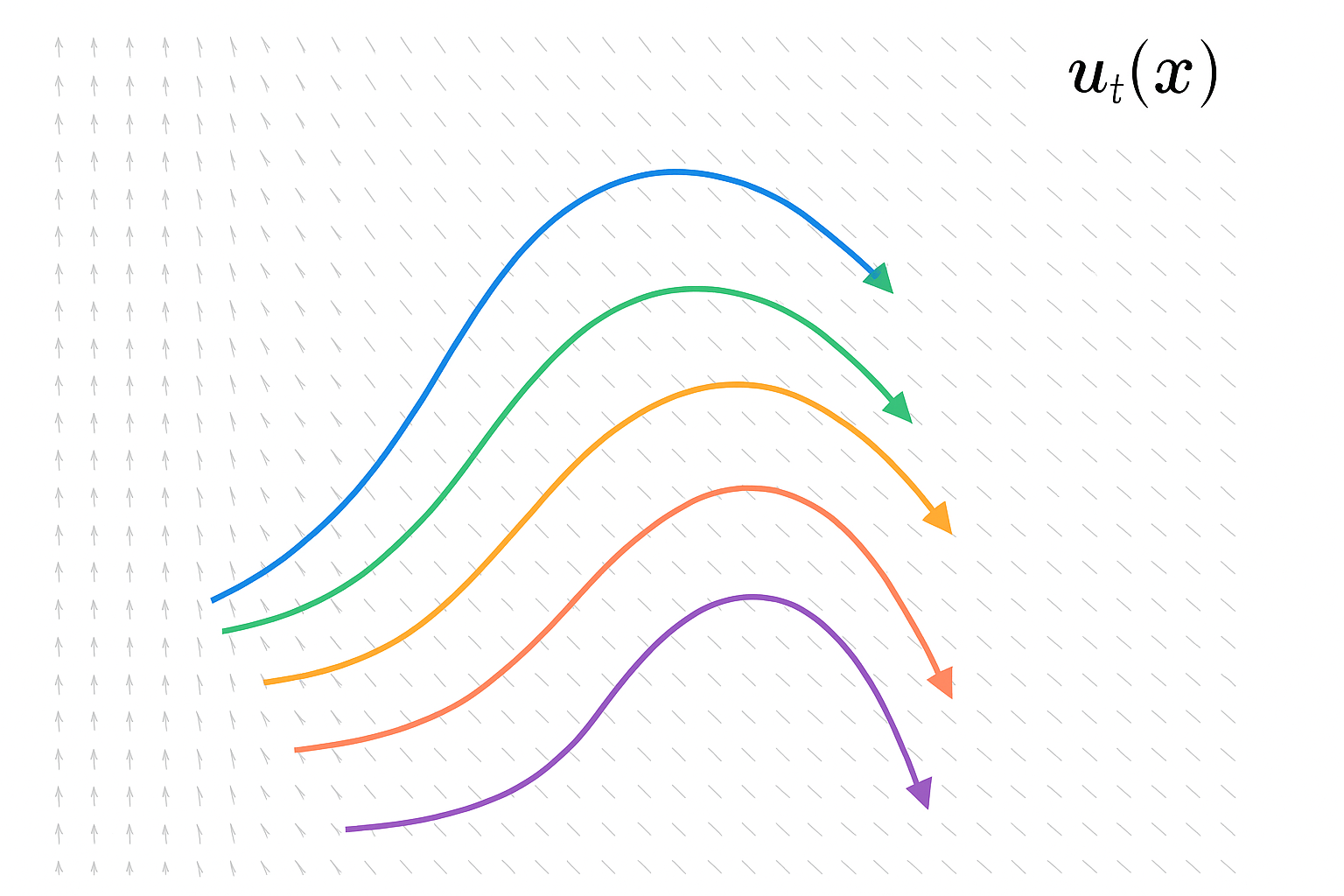
But what if we want to know the answer for any starting point? That’s the flow \(\phi_t(x)\): a function that takes any starting position \(x\) and returns where it ends up at time \(t\).

\[ X_t = \phi_t(x_0) \]

For one specific starting point \(x_0\), the trajectory and flow give the same answer. But the flow is more general — it’s the entire “transformation rule” for all points.

Figure 2: Multiple trajectories: the flow describes where ANY starting point ends up

Flow Equation

Since the flow satisfies the ODE, we can substitute \(X_t = \phi_t(x_0)\):

\[ \begin{aligned} \frac{dX_t}{dt} &= u_t(X_t) \implies \frac{d \phi_t(x_0)}{dt} = u_t(\phi_t(x_0)) \\ X_0 &= x_0 \implies \phi_0(x_0) = x_0 \end{aligned} \tag{2}\]

The second line says: at \(t=0\), every point is where it started (the flow is the identity map).

Summary

Concept	Notation	What it answers
Vector field	\(u_t(x)\)	“What direction should I move at position \(x\)?”
Trajectory	\(X_t\)	“Where is this one particle at time \(t\)?”
Flow	\(\phi_t(x)\)	“Where does any point \(x\) end up at time \(t\)?”

Vector fields define ODEs whose solutions are flows.

Think of it like Google Maps:

• Vector field = Traffic directions at every location (“turn left here”, “go straight there”)
• ODE = The instruction “just follow the GPS”
• Trajectory = The route YOUR car takes
• Flow = If 1000 cars started at different places and all followed GPS, the flow tells you where ALL of them end up

So: arrows (vector field) + “follow the arrows” (ODE) = everyone’s destination (flow).