USACO S1.3 Mixing Milk 贪心证明

将牛奶单价以不递减顺序排列：P={A1，A2，A3，…,An} 贪心规则： 按牛奶单位价格重小到大选择卖家且其储存量>0，每次若所需量>=该卖家可供给量则全部买完，否则仅买所需量，所需量=0到此结束。 证明归纳基础：至少有一个最优解包含选择1. 设：第i个卖家的供给量表示为Di，一最优解的选择序列M={j,j+1,j+2,…k}(1<j<=k<=n) 则该最优解总花费: 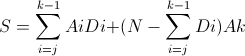设另一解的选择序列M’=M-{j} \(\cup\) {1} 则M’的花费为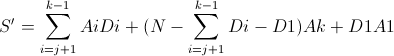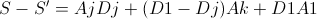： 若 D1>DJ: 设P=D1-Dj S-S’=D1(A1+Aj)+P(Ak-Aj) 因为价格>=0，,可供给量>=0,Ak>=Aj,所以S-S’>=0 若D1<=Dj 设P=Dj-D1 S’-S=P(Aj-Ak)+D1(Aj+A1)>=0 综上所述，M’比最优解M更优或者相等， 且因为M’比M更优与假设矛盾，所以最优解必定包含选择1. 证明归纳步骤： 假设前k不选择可以达到最优 设最优选择序列A={i1,i2,i3,…,ik}\(\cup\)B B为剩余子问题的某个最优解，根据归纳基础，B中必定包含在剩余子问题中存在选择1，设其位\(i_{k+1}\) 所以A={\(i_1,i_2,i_3,...,i_k\)}\(\cup\)B={\(i_1,i_2,i_3,...,i_k,i_{k+1}\)}\(\cup\){B-{\(i_{k+1}\)}} 所以第k+1步选择也可以导致最优解。 证毕。