向量的向量积

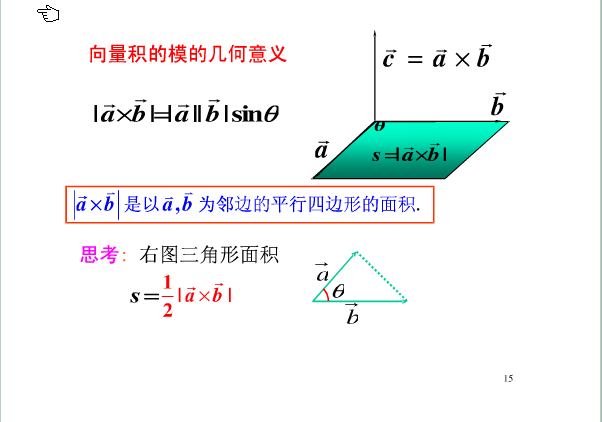
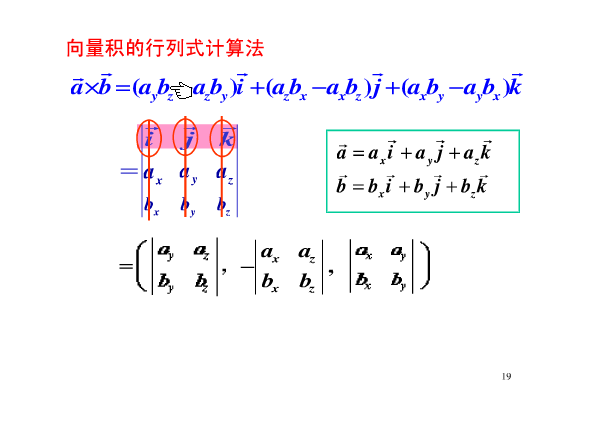笔记： 向量的大小：\(delim{|}{vec{a}}{|}delim{|}{vec{b}}{|}s\in theta\) 向量的方向：右手螺旋法则 1.行列式的记法：计算i向量，遮住i向量，向右走，计算j向量，遮住j向量，继续向右走，走到头回到第一个，以此类推，这样子j向量表示不用加负号。 2.\(vec{a}\)·(\(vec{b}*vec{c}\))=(\(vec{a}*vec{b}\))·\(vec{c}\) 用以向量a,b,c出发的平行六面体体积来理解，两式是从不同角度观察。 3.\(vec{a}*\)(\(vec{b}*vec{c}\))=(\(vec{a}\)·\(vec{c}\))\(vec{b}-\)(\(vec{a}\)·\(vec{b}\))\(vec{c}\) 4.判断三向量（三点)共面：\(vec{a}\)·\(delim{|}{vec{b}*vec{c}}{|}=0\) 理解：平行六面体体积为零，三向量一定在一个平面。