裴蜀定理
imported
notes
对任意两个整数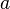 、
、 ,设
,设 是它们的最大公约数。那么关于未知数
是它们的最大公约数。那么关于未知数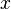 和
和 的线性丢番图方程(称为裴蜀等式 ):
的线性丢番图方程(称为裴蜀等式 ):
有整数解(x ,y) 当且仅当 m 是 d 的倍数。裴蜀等式有解时必然有无穷多个解。 证明: 如果 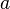 和
和  中有一个是0,比如
中有一个是0,比如 ,那么它们两个的最大公约数是
,那么它们两个的最大公约数是 。这时裴蜀等式变成
。这时裴蜀等式变成 ,它有整数解(x ,y) 当且仅当 m 是 d 的倍数,而且有解时必然有无穷多个解,因为
,它有整数解(x ,y) 当且仅当 m 是 d 的倍数,而且有解时必然有无穷多个解,因为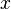 可以是任何整数。定理成立。 以下设
可以是任何整数。定理成立。 以下设 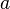 和
和  都不为0。 设
都不为0。 设 ,下面证明
,下面证明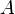 中的最小正元素是
中的最小正元素是 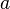 与
与  的最大公约数。 这个证明复杂且怪异,个人推荐算导上的证明,详情请见:http://localhost:8080/?p=581 在方程
的最大公约数。 这个证明复杂且怪异,个人推荐算导上的证明,详情请见:http://localhost:8080/?p=581 在方程 中,如果
中,如果  ,那么方程显然有无穷多个解:
,那么方程显然有无穷多个解:
这里附上通解公式:$(x_0-bt,y_0+at )$(t∈$\mathbb{Z}$)
关于通解公式推导请见:[http://localhost:8080/?p=622](http://localhost:8080/?p=622)
个人认为这里的“显然”太简略,无穷性可根据通解公式得出。
参考资料:[http://zh.wikipedia.org/wiki/%E8%A3%B4%E8%9C%80%E5%AE%9A%E7%90%86](http://zh.wikipedia.org/wiki/%E8%A3%B4%E8%9C%80%E5%AE%9A%E7%90%86) 并加以修改