算法导论第26章网络流 引理26.1证明

引理26.1 设G=(V,E)是一个网络流，f是G中的一个流。那么下列等式成立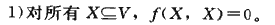： 证明： 设点a,b\(\in\)X,根据反对称性f(a,b)=-f(b,a),且f(X,X)中有X中元素数目个组{f(a,b),f(b,a)|a,b\(\in\)X},所以总和为0，引理成立。 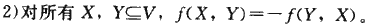证明： f(X,Y)=\(\sum{x \in X}{}{\sum{y \in Y}{}{f(x,y)}}\) =\(\sum{x \in X}{}{\sum{y \in Y}{}{-f(y,x)}}\) =-f(Y,X) 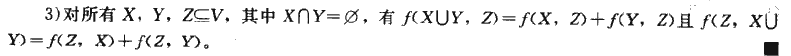证明： f(X\(\cup\)Y,Z)=\(\sum{x \in X}{}{f(x,Z)}+\sum{x \in Y}{}{f(x,Z)}\) f(X,Z)=\(\sum{x \in X}{}{f(x,Z)},f(Y,Z)=\sum{x \in Y}{}{f(x,Z)}\) 所以f(X\(\cup\)Y,Z)=f(X,Z)+f(Y,Z)。 另一个等式同理。